최종 수정 일자: 2020-06-14 15:51
해당 카테고리에 작성되는 글은 Introduction to Machine Learning with Python(파이썬 라이브러리를 활용한 머신 러닝)을 기반으로 작성되었습니다.

결정 트리(decision tree)는 분류와 회귀에 널리 사용되는 모델로 마치 스무고개처럼 어떠한 결정에 이르는 if/else 제어문들의 계층구조를 학습합니다. 예를 들어 매, 펭귄, 돌고래, 곰을 구분하는 질문 트리를 구성해봅시다.
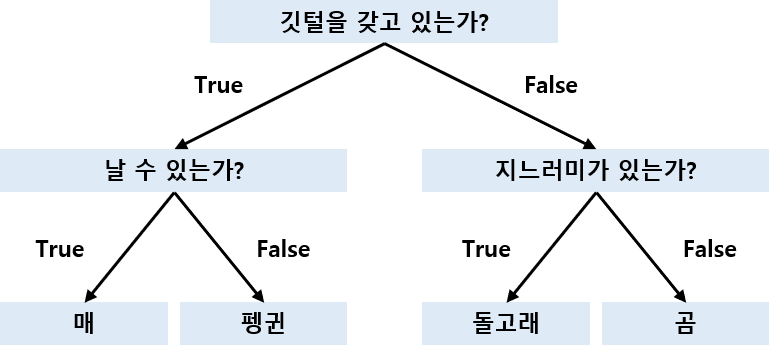
결정 트리 만들기
결정 트리의 학습은 정답에 가장 빨리 도달하는 일련의 if/else 질문을 학습하는 것입니다. 머신 러닝에서 이 질문들을 test라고 부릅니다. 일반적으로 위의 예시처럼 yes/no의 특성으로 데이터가 구성되어 있지는 않으며, 아래의 그림과 같이 특성이 연속적인 값을 갖는 경우가 많습니다. 따라서 test는 “a값보다 특성값 i가 더 큰가?”와 같은 식으로 만들어집니다.
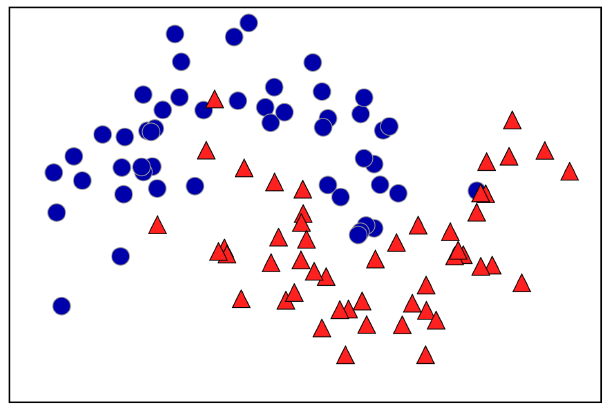
트리를 만들기 위해서 알고리즘은 모든 가능한 test에 대해 탐색하고 목표값에 가장 유익한 test를 찾습니다. 다음의 그림은 첫 번째 test가 결정된 상태를 보여줍니다.

데이터 셋을 x[1]=0.0596을 기준으로 수직으로 나누는 것이 가장 많은 정보를 제공합니다. 다시 말해 class 0의 데이터 포인트들을 class 1의 데이터 포인트로부터 가장 잘 분리합니다. 가장 위의 노드(node)를 root라 하며 전체 데이터 셋을 대표합니다. 즉, class 0에 속한 75개의 데이터 포인트와 class 1에 속한 75개의 데이터 포인트로 구성되어 있습니다. test가 True라면 해당 데이터 포인트는 왼쪽 노드로 할당되며 False라면 오른쪽 노드로 할당됩니다. 왼쪽 노드는 class 0에 속한 두 개의 데이터 포인트와 class 1에 속한 32개의 데이터 포인트를 포함합니다. 오른쪽 노드는 class 0에 속한 48개의 데이터 포인트와 class 1에 속한 18개의 데이터 포인트를 포함합니다. 이 두 노드는 위의 그림의 상단과 하단에 해당되며 하단 영역에는 여전히 class 0에 속한 데이터 포인트가 있으며 상단 영역에도 여전히 class 1에 속한 데이터 포인트가 있습니다. 좀 더 정확한 모델은 최선의 test를 각 영역에서 찾는 행위를 반복함으로써 얻어질 수 있습니다. 다음의 그림은 다음으로 이뤄진 가장 유익한 분리를 보여줍니다.
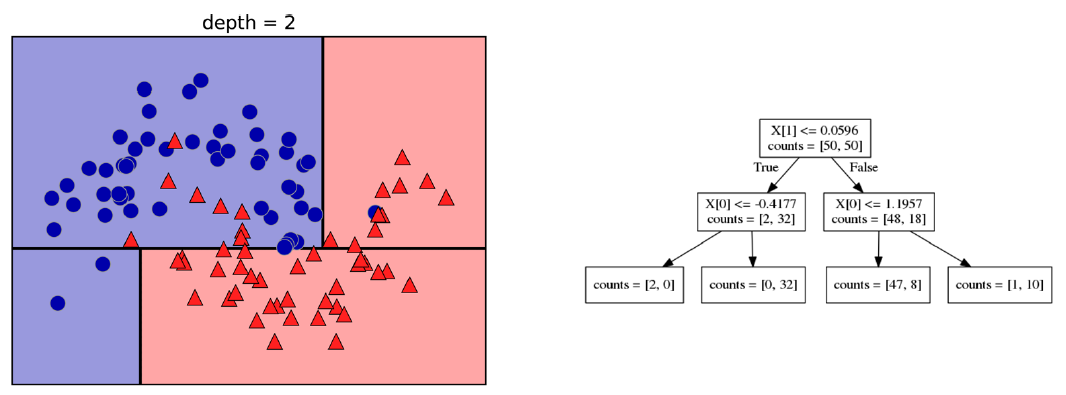
이러한 반복적인 과정은 결정들로 이뤄진 이진 트리를 만들게 되며, 각 노드는 test를 포함하게 됩니다. 이 과정은 각 영역이 오직 한 목표값(단일 class 또는 단일 회귀값)을 포함할 때까지 반복됩니다. 오직 같은 목표값만을 공유하도록 만들어진 영역을 ‘pure’하다고 합니다. 최종 결과는 다음의 그림에서 확인할 수 있습니다.


새로운 데이터 포인트에 대한 예측은 특성 공간의 분리 영역(leaf)에서 해당 포인트가 어디에 놓이는지에 의해서 결정됩니다. 포인트가 놓이는 영역은 트리의 root에서부터 시작하여 좌측에서 우측으로 가면서 알고리즘을 따라 결정됩니다.
이런 결정 트리를 회귀 문제에 사용하는 것도 가능합니다. 정확히 같은 테크닉을 사용하며 예측을 하는 과정에서 트리를 따라 새로운 데이터 포인트가 놓이게 될 영역을 찾습니다. 이 데이터 포인트에 대한 예측값은 영역 내 존재하는 데이터 포인트의 결과값의 평균치로 예측하게 됩니다.
결정 트리의 모델 복잡도 조절
모든 leaf를 pure한 상태로 만들 때까지 트리를 만드는 것은 매우 복잡한 모델링을 의미하며 학습 데이터 셋에 과대 적합한 모델을 만들게 됩니다. 즉, 학습 데이터 셋에 대해서는 100%의 정확도를 갖는 모델이 되어버리는 것이죠. 이와 같은 과대 적합을 막는 전략으로는 두 가지가 있습니다. 우선 트리의 생성을 적절한 때에 그만두는 것을 생각할 수 있습니다. 이를 pre-pruning이라 하며 트리의 최대 깊이를 제한하는 전략입니다. 다음으로는 정보가 거의 없는 노드를 제거하는 것을 생각해볼 수 있습니다. 이를 post-pruning이라 합니다. scikit-learn 패키지는 pre-pruning만 사용 가능합니다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(random_state=0) tree.fit(X_train, y_train) print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train))) print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test))) |
결과)
| Accuracy on training set: 1.000 Accuracy on test set: 0.937 |
예상대로 학습 데이터 셋의 정확도는 100%가 나오며, 이는 각 leaf가 pure한 상태가 되기 때문입니다. 결정 트리의 학습 깊이를 제한하지 않으면 과대 적합이 발생하며 새로운 데이터에 대한 일반화가 잘 이뤄지지 않을 수 있습니다. 이제 트리에 pre-pruning 전략을 적용해봅시다. 한 가지 옵션은 트리가 특정 깊이에 도달한 이후 학습을 멈추는 것입니다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(max_depth=4, random_state=0) tree.fit(X_train, y_train) print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train))) print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test))) |
결과)
| Accuracy on training set: 0.988 Accuracy on test set: 0.951 |
결정 트리 분석하기
tree 모듈로부터 export_graphviz를 이용하여 트리를 시각화할 수 있습니다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(max_depth=4, random_state=0) tree.fit(X_train, y_train) from sklearn.tree import export_graphviz data = export_graphviz(tree, out_file="tree.dot", class_names=["malignant", "benign"], feature_names=cancer.feature_names, impurity=False, filled=True) import graphviz with open("tree.dot") as f: dot_graph = f.read() graphviz.Source(dot_graph) |
결과) 문제 있음. 해결 중...
트리의 시각화는 알고리즘의 예측 방식을 잘 보여주며, 비전문가에게도 설명할 수 있을 정도로 쉬운 머신 러닝 알고리즘의 한 예라는 것을 보여줍니다. 각 노드의 n_samples는 해당 노드의 샘플 데이터의 수를 말하며 value는 class 별 샘플 데이터의 수를 말합니다.
트리 내 특성의 중요도
트리 전체를 관찰하는 것도 도움이 되지만 간단하게 트리의 작동을 요약할 수 있는 유용한 특징들이 몇몇 있습니다. 가장 일반적으로 사용되는 요약 방법이 바로 특성 중요도(feature importance)입니다. 특성 중요도는 결정 트리를 만드는 데 있어 각 특성이 얼마나 중요한지를 순위를 매깁니다. 각 특성별로 0과 1사이의 값을 가지며 0은 트리를 만드는데 전혀 사용되지 않은 특성을, 1은 목표를 완벽하게 예측하는 특성을 말합니다. 특성 중요도의 합은 항상 1로 고정됩니다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(max_depth=4, random_state=0) tree.fit(X_train, y_train) print("Feature importance:\n{}".format(tree.feature_importances_)) |
결과)
| Feature importance: [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.01019737 0.04839825 0. 0. 0.0024156 0. 0. 0. 0. 0. 0.72682851 0.0458159 0. 0. 0.0141577 0. 0.018188 0.1221132 0.01188548 0. ] |
또한 이를 시각화할 수 있습니다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(max_depth=4, random_state=0) tree.fit(X_train, y_train) def plot_feature_importances_cancer(model): n_features = cancer.data.shape[1] plt.barh(range(n_features), model.feature_importances_, align='center') plt.yticks(np.arange(n_features), cancer.feature_names) plt.xlabel("Feature importance") plt.ylabel("Feature") plot_feature_importances_cancer(tree) plt.show() |
결과)

이로부터 “worst radius”가 가장 중요한 특성임을 확인할 수 있습니다. 그러나 어떤 특성이 낮은 특성 중요도를 갖는다고 해서 해당 특성이 유용한 정보를 주지 못한다는 것은 아닙니다. 그저 트리에 의해서 선택 받지 못했을 뿐입니다. Linear model에서의 계수와는 달리 특성 중요도는 항상 양수입니다.
| tree = mglearn.plots.plot_tree_not_monotone() plt.show() |
결과)

| Feature importances: [0. 1.] |
위의 그래프는 두 개의 특성과 두 개의 class를 갖는 데이터 셋을 보여줍니다. 모든 정보는 x[1]에 담겨있으며, x[0]은 전혀 사용되지 않습니다. 그러나 x[1]과 output class 사이의 관계는 단조롭지만은 않습니다. 이를 두고 “높은 값의 x[0]이 class 0을 의미하며 낮은 값의 x[0]은 class 1을 의미한다”고 말할 수 없습니다.
이제 회귀 문제를 결정 트리를 이용하여 모델링해봅시다. 이번엔 DecisionTreeRegressor와 LinearRegression 두 모델을 비교해봅시다. 사용할 데이터는 역사적으로 기록된 RAM 가격의 변화이며, 2000년 이전의 데이터로부터 학습한 모델링을 통해 2000년 이후의 가격을 예측한 뒤 점수를 매겨봅시다. 가격을 로그 스케일로 다시 스케일링하여 상대적으로 선형적인 관계를 만든 뒤 모델링을 시작합니다. 실제로 이러한 리스케일링은 DecisionTreeRegressor의 결과에 전혀 영향을 미치지 않습니다만 LinearRegression에 큰 영향을 미칩니다.
| import os ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv")) # use historical data to forecast prices after the year 2000 data_train = ram_prices[ram_prices.date < 2000] data_test = ram_prices[ram_prices.date >= 2000] # predict prices based on data X_train = data_train.date[:, np.newaxis] # we use a log-transform to get a simpler relation of data to target y_train = np.log(data_train.price) from sklearn.tree import DecisionTreeRegressor tree = DecisionTreeRegressor().fit(X_train, y_train) from sklearn.linear_model import LinearRegression linear_reg = LinearRegression().fit(X_train, y_train) # predict on all data X_all = ram_prices.date[:, np.newaxis] pred_tree = tree.predict(X_all) pred_lr = linear_reg.predict(X_all) # undo log-transform price_tree = np.exp(pred_tree) price_lr = np.exp(pred_lr) plt.semilogy(data_train.date, data_train.price, label="Training data") plt.semilogy(data_test.date, data_test.price, label="Test data") plt.semilogy(ram_prices.date, price_tree, label="Tree prediction") plt.semilogy(ram_prices.date, price_lr, label="Linear prediction") plt.legend() plt.show() |
결과)

Linear model은 데이터를 선으로 근사하며 학습 데이터 셋의 세밀한 변화에 대해서는 넘어가지만 2000년 이후의 가격에 대해서도 어느정도 잘 맞추는 결과를 보입니다. 그러나 트리 모델은 학습 데이터에 대한 예측은 완벽히 이뤄집니다만, 이는 모델 복잡도를 조절하지 않아서 그런것이며 그렇다 하더라도 2000년 이후의 가격은 전혀 예측하지 못합니다. 트리는 새로운 응답을 만들어내는 능력은 없습니다. 다시 말해, 학습 데이터 셋을 벗어나는 예측은 불가능합니다.
장점, 단점, 매개변수
모델 복잡도를 조절하는 매개 변수로 pre-pruning 매개 변수가 있었습니다. 적당한 pre-pruning 전략을 고르는 것만으로도 overfitting을 막을 수 있었습니다. 주로 max_depth, max_leaf_nodes, min_samples_leaf를 설정하여 과대 적합을 막습니다.
결정 트리는 다른 알고리즘에 비해 두 가지 장점이 있습니다. 첫 째, 결과 모델의 시각화가 쉬우며 비전문가도 이해할 수 있다는 것입니다. 둘 째, 데이터의 scaling에 영향을 받지 않는다는 것입니다. 즉, normalization이나 standardization이 전혀 필요하지 않습니다. 특히 결정 트리는 완전히 다른 스케일을 갖는 특성들을 보유한 데이터, 또는 이진 특성과 연속 특성을 모두 보유한 데이터에서도 잘 작동합니다.
결정 트리의 단점은 pre-pruning을 이용한다 하더라도 과대 적합 및 좋지 않은 일반화 성능을 보이는 경향이 있습니다. 따라서 대부분의 경우, 다음에 다룰 ensemble method이 사용됩니다.
'Python-머신 러닝 > Python-지도 학습 알고리즘' 카테고리의 다른 글
| 2. 지도 학습 알고리즘 (6) Ensembles of Decision Trees (Gradient Boosted Regression Trees) (0) | 2020.06.14 |
|---|---|
| 2. 지도 학습 알고리즘 (5) Ensembles of Decision Trees (Random Forest) (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘 (3) Naive Bayes Classifiers (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘 (2) Linear Model (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘 (1) k-Nearest Neighbors (k-NN) (0) | 2020.06.14 |