최종 수정 일자: 2020-06-14 15:33
해당 카테고리에 작성되는 글은 Introduction to Machine Learning with Python(파이썬 라이브러리를 활용한 머신 러닝)을 기반으로 작성되었습니다.

Linear model, 다른 말로 선형 모델은 실제로 많이 사용되는 모델로 학습 데이터 셋의 입력 특성들의 선형 함수(linear function)을 이용하여 예측하는 모델입니다.
Linear model 회귀(regression)
직관적으로 linear model은 회귀 문제를 통해 이해하는 것이 쉬우므로 회귀 문제에서의 linear model을 이용한 머신 러닝부터 살펴봅시다. Linear model에 대한 일반적인 예측 공식은 다음과 같습니다.

x[0] ~ x[p]는 한 데이터 포인트의 각 특성(feature)에 대한 값을 지시하며 따라서 이 예시에서 feature의 수는 p + 1개가 됩니다. w와 b는 학습을 통해 만들어지는 모델의 매개변수이며 y\hat은 모델을 통해서 만들어지는 예측 결과값입니다. 특성이 하나인 데이터 셋에 대해서는

와 같이 예측 공식이 만들어지며, 이는 중학교 수학 시간에 배웠던 일차함수 형태임을 쉽게 알 수 있습니다. 즉, w[0]은 기울기가 되며 b는 y축 절편이 됩니다. 특성의 수가 늘어남에 따라서 w[0], w[1], …과 같이 각 특성값에 곱해지는 w가 늘어나게 되는데, 각각 해당 특성을 제외한 나머지 특성을 고정시켜 놓은 채 그 특성을 변화시켜갈 때 나타나는 기울기라고 생각하면 됩니다. 또는 해당 특성이 예측값에 미치는 무게치라고 생각해도 됩니다.
일차원 데이터 셋인 wave 데이터 셋을 통해 w[0]과 b에 대해서 배워봅시다.
| mglearn.plots.plot_linear_regression_wave() plt.show() |
결과)

| w[0]: 0.393906 b: -0.031804 |
그래프 위의 직선은 약 0.4 정도, 즉 w[0]의 기울기를 가지면서 움직입니다. 해당 특성이 결과값을 예측하는데 기여하는 정도를 의미하기 때문입니다. y축 절편은 0에 가까우며 이는 모델링 결과 b값이 -0.03정도로 나타나기 때문입니다.
회귀 문제에 대한 linear model은 단일 특성에 대해서는 선형, 두 개의 특성에 대해서는 평면, 더 높은 차원의 데이터 셋에 대해서는 초평면(hyper plane)으로 예측이 이뤄지게 됩니다. figure_9의 KNeighborRegressor와 비교해보면, 예측을 하기 위해 일직선의 결과를 이용하는 것이 데이터의 디테일한 측면을 무시하는 것처럼 보여서 거부감이 있을 수 있습니다. 이는 일정 부분 맞는 말입니다만, 일차원의 데이터 셋이기 때문에 더욱 그래보입니다. Linear model은 특성의 수가 많아질수록 강력해집니다. 특히 학습 데이터 포인트보다 많은 특성을 갖는 경우, 어떤 결과값 y이라도 완벽하게 (학습 데이터 셋에 대해서) 선형 함수로 모델링될 수 있습니다.
회귀 문제 해결을 위한 linear model에는 여러 가지가 있습니다. 이들은 모델의 매개변수인 w와 b를 학습 데이터 셋으로부터 어떻게 학습하는지에 따라, 또 모델 복잡도가 어떻게 조절되는지에 따라 달라집니다. 여기서는 가장 널리 알려진 선형 회귀 모델에 대해서 살펴보겠습니다.
Linear model 회귀(regression, 최소 제곱 추정)
선형 회귀(linear regression), 또는 최소 제곱(ordinary least square, OLS) 추정은 회귀 문제에 대한 가장 단순하면서도 고전적인 선형 방법론입니다. 선형 회귀 분석은 학습 데이터로부터 얻어지는 예측값과 실제값 사이의 평균 제곱 오차(mean squared error)가 최소가 되도록 w와 b를 선택합니다. 평균 제곱 오차란, 예측값과 실제값 사이의 차이의 제곱의 합으로 나타납니다. 선형 회귀 모델은 매개변수가 없으며, 이는 일종의 장점일수도 있습니다만, 모델 복잡도를 조절할 수 있는 수단이 없다는 뜻이기도 합니다.
| from sklearn.linear_model import LinearRegression X, y = mglearn.datasets.make_wave(n_samples=60) from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42) lr = LinearRegression().fit(X_train, y_train) print("lr.coef_:{}".format(lr.coef_)) print("lr.intercept_:{}".format(lr.intercept_)) print("Training set score: {:.2f}".format(lr.score(X_train, y_train))) print("Test set score: {:.2f}".format(lr.score(X_test, y_test))) |
결과)
| lr.coef_:[0.39390555] lr.intercept_:-0.031804343026759746 Training set score: 0.67 Test set score: 0.66 |
lr.coef_는 기울기 매개변수인 w를 말하며 무게(weight) 또는 계수(coefficient)라고 합니다. lr.intercept_는 y축 절편인 오프셋(offset)을 말하며 절편(intercept)이라고 합니다. intercept_는 항상 단일 부동 소수점 숫자형 데이터이지만 coef_는 Numpy 배열 데이터입니다. 단일 특성을 갖는 데이터 셋에 대한 학습 결과이므로 [0.39390555]와 같이 나타나지만, 특성이 여러 개인 데이터 셋의 경우 각 특성에 대한 기울기가 모두 배열 안에 포함되어 있는 형식으로 나타납니다.
k-NN 회귀 모델과 마찬가지로 LinearRegression().fit() 클래스 내의 score 메서드는 R2 값을 의미합니다. R2 = 0.66은 그렇게 좋은 결과는 아니지만 학습 데이터 셋과 시험 테스트 셋의 값이 거의 비슷한 것을 알 수 있습니다. 이는 과소 적합(underfitting)의 가능성을 의미합니다. 일차원 데이터 셋을 이용할 때는 모델이 매우 단순하기 때문에 과대 적합(overfitting)의 문제가 생길 가능성은 거의 없습니다. 높은 차원의 데이터 셋을 이용할 경우, linear model은 매우 강력해지지만 과대 적합의 문제가 생길 가능성이 더 높습니다. Boston Housing 데이터 셋을 통해 이를 확인해봅시다. 불러올 데이터 셋은 단순 Boston Housing 데이터 셋이 아닌, 특성들 사이의 곱들을 새로운 특성으로 저장하여 506개의 데이터 포인트와 105개의 특성을 가진 확장된 데이터 셋입니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import LinearRegression lr = LinearRegression().fit(X_train, y_train) print("Training set score: {:.2f}".format(lr.score(X_train, y_train))) print("Test set score: {:.2f}".format(lr.score(X_test, y_test))) |
결과)
| Training set score: 0.95 Test set score: 0.61 |
학습 데이터 셋에 대한 높은 성능과 시험 데이터 셋에 대한 낮은 점수는 과대 적합이 되었다는 뜻입니다. 따라서 모델 복잡도를 조절할 수 있는 모델을 찾아야할 필요가 생겼습니다. 이때 가장 일반적으로 사용하는 표준 선형 회귀 모델이 ridge regression 입니다.
Ridge Regression
Ridge regression은 마찬가지로 회귀 문제에 대한 linear model이며, 최소 제곱 추정에서 사용한 예측 공식과 같은 것을 사용합니다. 다른 점은 ridge regression에서 계수 w가 학습 데이터를 잘 예측할 뿐만 아니라 추가적인 제약 조건에도 잘 맞게 선택된다는 것입니다. 계수들이 가능한한 작게 설정되며 이는 0에 가깝게, 즉 최대한 작은 기울기를 갖도록 설정됩니다. 이러한 제약 조건은 정규화(regularization)의 한 예입니다. 정규화는 과대 적합을 피하기 위해 모델을 제한하는 것으로 ridge regression에서 사용하는 정규화를 L2 정규화라 합니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Ridge ridge = Ridge().fit(X_train, y_train) print("Training set score: {:.2f}".format(ridge.score(X_train, y_train))) print("Test set score: {:.2f}".format(ridge.score(X_test, y_test))) |
결과)
| Training set score: 0.89 Test set score: 0.75 |
Ridge의 학습 데이터 셋 점수가 LinearRegression보다는 낮지만 시험 데이터 셋의 점수는 더 높은 것을 알 수 있습니다. 즉, 과대 적합의 가능성을 낮춘 것입니다. 덜 복잡한 모델은 학습 데이터 셋에 대해서는 성능이 낮을 수도 있지만, 일반화를 더 잘합니다. 일반화 성능만 고려한다면 이 경우 LinearRegression 모델에 비해 Ridge 모델을 선택하는 것이 더 낫습니다.
Ridge 모델은 모델의 복잡도와 학습 데이터 셋에 대한 성능 사이에 trade-off 관계가 있습니다. 학습 데이터 셋에 대한 성능에 비해 모델의 복잡도에 어느 정도 중정을 두느냐는 사용자에 따라 달라지며 이를 alpha 매개변수를 통해 조절할 수 있습니다. 기본적으로 따로 설정하지 않으면 alpha=1.0으로 설정되어 있으며 최적의 alpha 값은 사용하는 데이터 셋에 따라 달라질 수 있습니다. alpha를 크게 하면 계수 w를 0에 더욱 가깝게 움직이게 하고 이는 학습 데이터 셋에 대한 성능은 떨어뜨리지만 일반화에 도움을 주게 됩니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Ridge ridge10 = Ridge(alpha=10).fit(X_train, y_train) print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train))) print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test))) |
결과)
| Training set score: 0.79 Test set score: 0.64 |
alpha를 작게 하면 계수 w를 덜 제한적으로 만들게 됩니다. 아주 작은 alpha를 설정하면 LinearRegrssion과 유사한 모델을 만들게 됩니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Ridge ridge01 = Ridge(alpha=0.1).fit(X_train, y_train) print("Training set score: {:.2f}".format(ridge01.score(X_train, y_train))) print("Test set score: {:.2f}".format(ridge01.score(X_test, y_test))) |
결과)
| Training set score: 0.93 Test set score: 0.77 |
이 데이터 셋에 대해서는 alpha=0.1이 잘 작동하는 것 같습니다. 이번에는 alpha 매개변수가 모델을 어떻게 바꾸는지 좀 더 정성적인 시각을 얻어봅시다. alpha값에 따라서 coef_를 조회하여 시각화 해봅시다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import LinearRegression lr = LinearRegression().fit(X_train, y_train) from sklearn.linear_model import Ridge ridge = Ridge().fit(X_train, y_train) ridge10 = Ridge(alpha=10).fit(X_train, y_train) ridge01 = Ridge(alpha=0.1).fit(X_train, y_train) plt.plot(ridge.coef_, 's', label="Ridge alpha=1") plt.plot(ridge10.coef_, '^', label="Ridge alpha=10") plt.plot(ridge01.coef_, 'v', label="Ridge alpha=0.1") plt.plot(lr.coef_, 'o', label="LinearRegression") plt.xlabel("Coefficient index") plt.ylabel("Coefficient magnitude") plt.hlines(0, 0, len(lr.coef_)) plt.ylim(-25, 25) plt.legend() plt.show() |
결과)
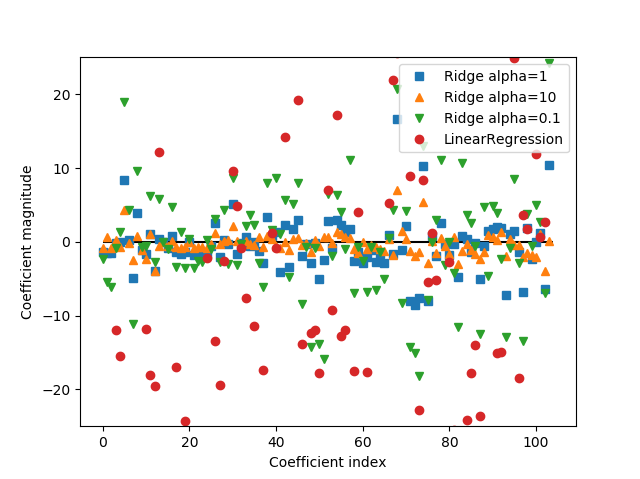
x축은 계수 w의 집합체(w[0], w[1], …, w[104])의 인덱스이며 y축은 각 계수가 어떤 값을 가지는지를 보여줍니다. alpha=10의 경우 계수들이 -3과 3 사이에서 움직이며 alpha=1일 때 좀 더 크게 움직입니다. alpha=0.1은 훨씬 더 큰 범위 내에서 계수가 움직입니다.
정규화의 영향을 이해하는 또 다른 방법은 alpha를 고정시켜 놓은 채 학습 데이터 셋의 수를 변화시켜 보는 것입니다. LinearRegression과 Ridge(alpha=1)에 대해 학습 데이터 사이즈를 변화시켜가면서 점수(R2)를 그려봅시다. 이러한 유형의 그래프를 learning curve라 합니다.
| mglearn.plots.plot_ridge_n_samples() plt.show() |
결과)
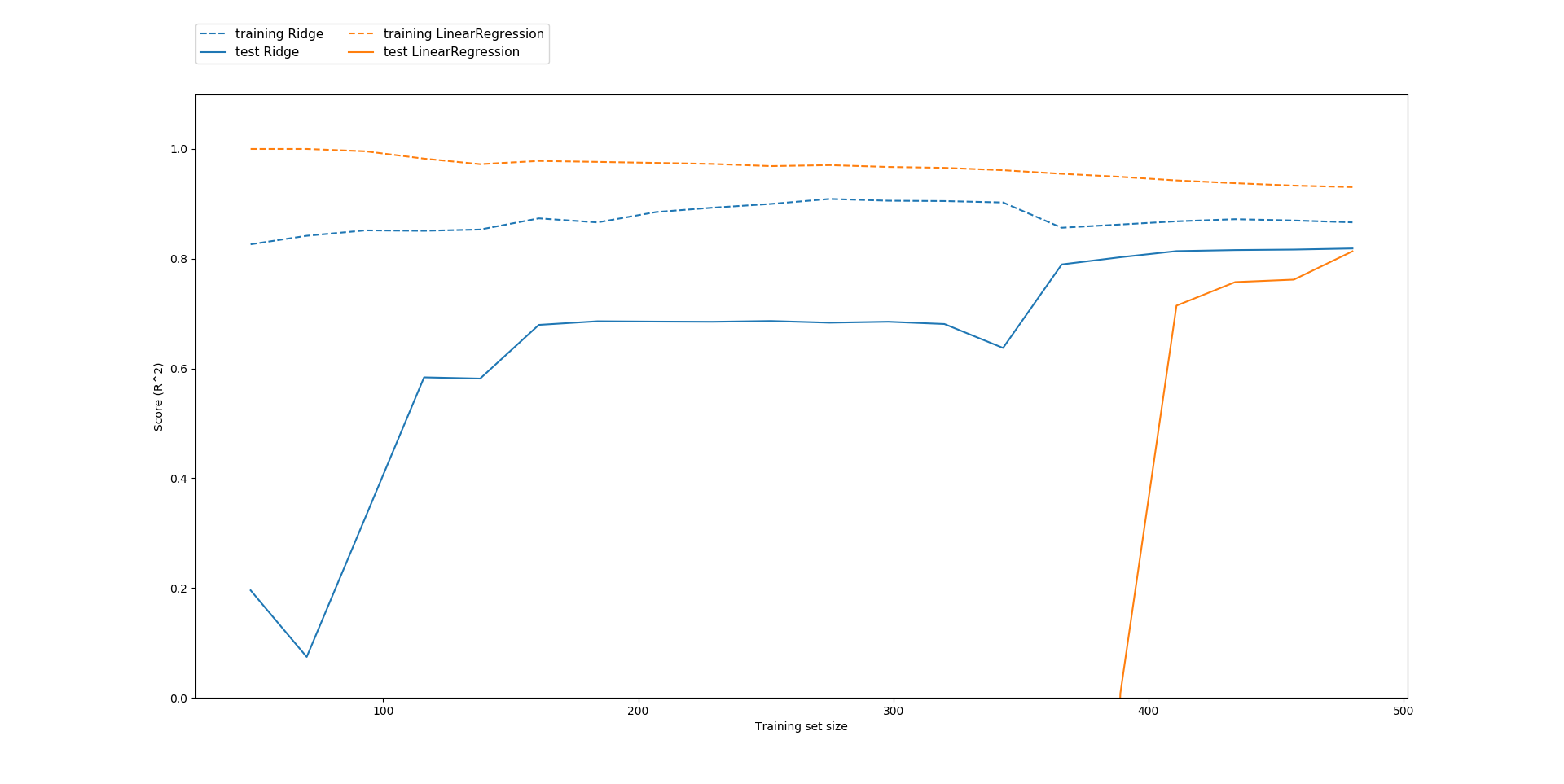
모든 학습 데이터 사이즈에 대해 학습 점수는 시험 점수보다 높습니다. Ridge가 정규화되어 있기 때문에 ridge의 학습 점수는 linear regression의 학습 점수보다 모든 구간에서 낮습니다. 그러나 시험 데이터에 대한 점수는 ridge가 더 나으며 특히 데이터의 수가 적을수록 그렇습니다. LinearRegression의 성능은 학습 데이터 셋의 크기가 커질수록 향상됩니다.
Lasso Regression
Ridge 이외에 선형 회귀를 정규화하는 모델로는 Lasso가 있습니다. Lasso는 ridge와는 다르게 L1 정규화 방식을 사용하는데, 계수를 0에 최대한 가깝게 하는 것은 물론, 일부 계수들을 0으로 만들어버립니다. 즉, 모델링에 필요한 특성들을 자동으로 선택하는 것입니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Lasso lasso = Lasso().fit(X_train, y_train) print("Training set score: {:.2f}".format(lasso.score(X_train, y_train))) print("Test set score: {:.2f}".format(lasso.score(X_test, y_test))) print("Number of features used: {}".format(np.sum(lasso.coef_ != 0))) |
결과)
| Training set score: 0.29 Test set score: 0.21 Number of features used: 4 |
결과만 놓고 보면 학습 데이터 셋과 시험 데이터 셋 모두에 대해 좋지 않은 성능을 보이는 것 같습니다. 일종의 과소 적합으로 해석할 수 있으며 이는 105개의 특성 중 4개의 특성만을 사용하여 모델링을 진행했기 때문입니다. Ridge와 마찬가지로 alpha라는 매개 변수를 통해 선형 회귀의 계수를 0에 가깝게 조절할 수 있으며 따로 설정해주지 않으면 기본 값은 alpha=1.0입니다. 과소 적합을 피하기 위해서는 alpha를 줄여야 합니다. 또한 실행할 최대 반복 횟수를 max_iter 설정을 통해 증가시켜봅시다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Lasso # we increase the default setting of "max_iter" # otherwise the model would warn us that we should increase max_iter. lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train) print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train))) print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test))) print("Number of features used: {}".format(np.sum(lasso001.coef_ != 0))) |
결과)
| Training set score: 0.90 Test set score: 0.77 Number of features used: 33 |
낮은 alpha 값은 더 복잡한 모델링을 제공하며 학습 데이터 셋과 시험 데이터 셋 모두에 대해 더 잘 작동하도록 합니다. 또한 Ridge와 비교해도 약간 성능이 더 좋으며 105개의 특성 중 33개만을 사용합니다. 그러나 alpha를 너무 낮게 설정하면 정규화의 효과가 없어지며 LinearRegression과 비슷한 결과를 얻게 됩니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Lasso lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train) print("Training set score: {:.2f}".format(lasso00001.score(X_train, y_train))) print("Test set score: {:.2f}".format(lasso00001.score(X_test, y_test))) print("Number of features used: {}".format(np.sum(lasso00001.coef_ != 0))) |
결과)
| Training set score: 0.95 Test set score: 0.64 Number of features used: 96 |
Ridge 모델과 비슷하게 coefficient의 인덱스에 대한 값들을 시각화할 수 있습니다.
| X, y = mglearn.datasets.load_extended_boston() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.linear_model import Ridge ridge01 = Ridge(alpha=0.1).fit(X_train, y_train) from sklearn.linear_model import Lasso lasso = Lasso().fit(X_train, y_train) lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train) lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train) plt.plot(lasso.coef_, 's', label="Lasso alpha=1") plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01") plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001") plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1") plt.legend(ncol=2, loc=(0, 1.05)) plt.ylim(-25, 25) plt.xlabel("Coefficient index") plt.ylabel("Coefficient magnitude") plt.show() |
결과)

alpha=1일 때 대부분의 계수가 0에 가까울 뿐만 아니라 남아 있는 계수들도 그 크기가 작은 것을 알 수 있습니다. alpha를 0.01에서 0.0001로 갈수록 모델은 비정규화되지만 대부분의 계수가 0이 아니며 크기가 커집니다. alpha=0.1인 Ridge 모델과 alpha=0.01인 Lasso 모델은 비슷한 성능을 보이지만 Ridge 모델은 0인 계수가 없다는 차이점이 있습니다.
실제로 두 알고리즘 중 Ridge를 우선적으로 선택합니다. 다만 특성이 너무 많거나 특정 중 유효한 것이 몇 개 없다고 생각될 때, 또는 해석이 쉬운 모델을 바랄 때 Lasso를 고려해봅니다.
Linear model 분류(classification)
직관적으로는 회귀 문제에 적합해보이는 linear model은 의외로 분류 문제에도 잘 사용됩니다. 이진 분류의 경우를 먼저 살펴봅시다. 이진 분류의 경우 예측은 아래의 공식을 이용해서 만들어집니다.

선형 회귀와 비슷해 보이지만 등호가 아닌 부등호가 있다는 것을 알 수 있습니다. 즉, 특성들의 계수 배의 합으로서 결과를 반환하는 것이 아니라, 예측값을 0으로 임계값을 설정합니다. 함수가 0보다 크다면 class-1로 분류하고 0보다 크다면 class+1로 분류함으로써 분류가 이루어집니다. 분류를 위한 linear model에서 결정 경계는 클래스를 구분하는 선/평면/초평면이 됩니다. 선형 회귀와 비슷하게 계수 w와 절편 b를 학습 데이터를 찾는 방식에 따라, 또 사용되는 정규화의 종류에 따라 알고리즘에 차이가 발생합니다.
기술적/수학적 문제로 알고리즘이 만들어내는 잘못된 분류의 수를 최소화하는 w와 b를 찾는 것은 불가능합니다. 가장 일반적인 두 가지 선형 분류 알고리즘은 logistic regression과 linear support vector machines (linear SVM)으로 각각 linear_model.LogisticRegression과 svm.LinearSVC로 실행됩니다. (SVC는 support vector classifier를 의미합니다) 이름만 보면 회귀에 적합한 알고리즘인 것 같지만 logistic regression은 분류 알고리즘입니다.
| X, y = mglearn.datasets.make_forge() fig, axes = plt.subplots(1, 2, figsize=(10, 3)) from sklearn.linear_model import LogisticRegression from sklearn.svm import LinearSVC for model, ax in zip([LinearSVC(), LogisticRegression()], axes): clf = model.fit(X, y) mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=.7) mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax) ax.set_title("{}".format(clf.__class__.__name__)) ax.set_xlabel("Feature 0") ax.set_ylabel("Feature 1") axes[0].legend() plt.show() |
결과)
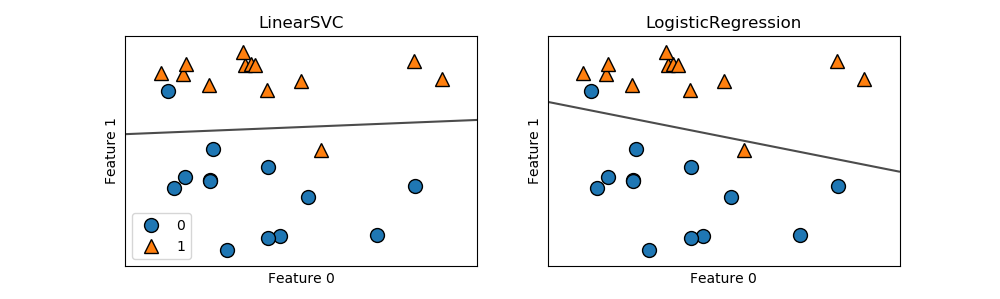
어떤 새로운 데이터든 검정색 실선 위에 찍히는 데이터는 class 1로 분류되며 실선 밑에 찍히는 데이터는 class 0으로 분류됩니다. 두 모델은 비슷한 결정 경계를 기본적으로 두 모델 모두 Ridge 알고리즘에서 사용했던 L2 정규화를 적용합니다.
LogisticRegression과 LinearSVC에서 정규화의 강도를 결정하는 trade-off 매개변수는 C입니다. C 값이 클수록 덜 정규화되며 이는 곧 학습 데이터 셋에 가능한 잘 맞추도록 모델링을 진행합니다. 낮은 값의 C를 선택하면 0에 가까운 계수 벡터 w를 찾습니다.
| mglearn.plots.plot_linear_svc_regularization() plt.show() |
결과)

작은 값의 C를 이용하면 알고리즘을 데이터 포인트의 다수에 조정되도록 학습시키며 큰 값의 C를 선택하면 각각의 개별 데이터가 정확하게 분류되도록 학습시킵니다.
회귀 문제의 경우와 비슷하게 낮은 차원의 데이터 셋보다는 높은 차원의 데이터 셋에서 강력함을 가집니다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.linear_model import LogisticRegression logreg = LogisticRegression(max_iter=100000).fit(X_train, y_train) print("Training set score: {:.3f}".format(logreg.score(X_train, y_train))) print("Test set score: {:.3f}".format(logreg.score(X_test, y_test))) |
결과)
| Training set score: 0.958 Test set score: 0.958 |
기본 설정값인 C=1도 꽤나 좋은 성능을 보여줍니다만 학습 데이터 셋의 성능과 시험 데이터 셋의 성능이 유사한 것으로 보아 과소 적합의 가능성이 있습니다. C를 증가시켜 모델 복잡도를 올려봅시다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.linear_model import LogisticRegression logreg100 = LogisticRegression(C=100, max_iter=100000).fit(X_train, y_train) print("Training set score: {:.3f}".format(logreg100.score(X_train, y_train))) print("Test set score: {:.3f}".format(logreg100.score(X_test, y_test))) |
결과)
| Training set score: 0.984 Test set score: 0.965 |
C를 작게 설정하여 더 정규화된 모델을 봅시다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.linear_model import LogisticRegression logreg001 = LogisticRegression(C=0.01, max_iter=100000).fit(X_train, y_train) print("Training set score: {:.3f}".format(logreg001.score(X_train, y_train))) print("Test set score: {:.3f}".format(logreg001.score(X_test, y_test))) |
결과)
| Training set score: 0.953 Test set score: 0.951 |
마지막으로 C값에 따라 계수 인덱스와 그 값이 어떻게 시각화 되는지를 봅시다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42) from sklearn.linear_model import LogisticRegression logreg = LogisticRegression(max_iter=100000).fit(X_train, y_train) logreg100 = LogisticRegression(C=100, max_iter=100000).fit(X_train, y_train) logreg001 = LogisticRegression(C=0.01, max_iter=100000).fit(X_train, y_train) plt.plot(logreg.coef_.T, 'o', label="C=1") plt.plot(logreg100.coef_.T, '^', label="C=100") plt.plot(logreg001.coef_.T, 'v', label="C=0.001") plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90) plt.hlines(0, 0, cancer.data.shape[1]) plt.ylim(-5, 5) plt.xlabel("Coefficient index") plt.ylabel("Coefficient magnitude") plt.legend() plt.show() |
결과)

Linear model 다중 분류(multiclass classification)
다중 분류(multiclass classification) 문제에서 선형 분류 알고리즘은 one-vs.-rest 접근법을 사용합니다. 즉 각 class에 대해 해당 class와 이외의 class를 기반으로 이진 분류 모델을 학습하여 다른 class로부터 해당 class를 분리하도록 시도합니다. 즉, 분류 class의 수만큼 이진 분류 모델을 만들게 됩니다. 다중 분류 logistic regression은 위와는 조금 다른 전략을 취하긴 하지만 결과적으로는 마찬가지로 각 class당 하나의 계수 벡터 w와 절편 b를 만듭니다.
| from sklearn.datasets import make_blobs X, y = make_blobs(random_state=42) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.xlabel("Feature 0") plt.ylabel("Feature 1") plt.legend(["Class 0", "Class 1", "Class 2"]) plt.show() |
결과)
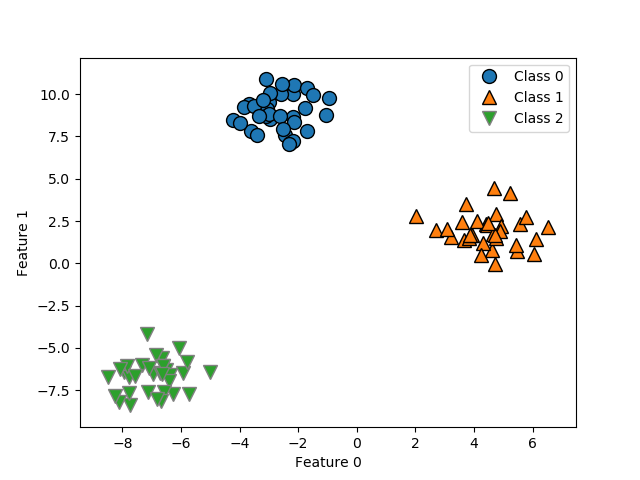
이제 LinearSVC 분류기를 이용해 학습시켜봅시다.
| from sklearn.datasets import make_blobs X, y = make_blobs(random_state=42) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) from sklearn.svm import LinearSVC linear_svm = LinearSVC().fit(X, y) print("Coefficient shape: ", linear_svm.coef_.shape) print("Intercept shape: ", linear_svm.intercept_.shape) |
결과)
| Coefficient shape: (3, 2) Intercept shape: (3,) |
coef_의 shape이 (3, 2) 즉, 세 개의 class와 두 개의 feature에 대해 각각 계수가 결정되었음을 말합니다. intercept_는 일차원 배열의 형태로 각 class에 대해 절편이 결정되었다는 것을 알 수 있습니다.
| from sklearn.datasets import make_blobs X, y = make_blobs(random_state=42) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) from sklearn.svm import LinearSVC linear_svm = LinearSVC().fit(X, y) line = np.linspace(-15, 15) for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']): plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color) plt.ylim(-10, 15) plt.xlim(-10, 8) plt.xlabel("Feature 0") plt.ylabel("Feature 1") plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1', 'Line class 2'], loc=(1.01, 0.3)) plt.show() |
결과)
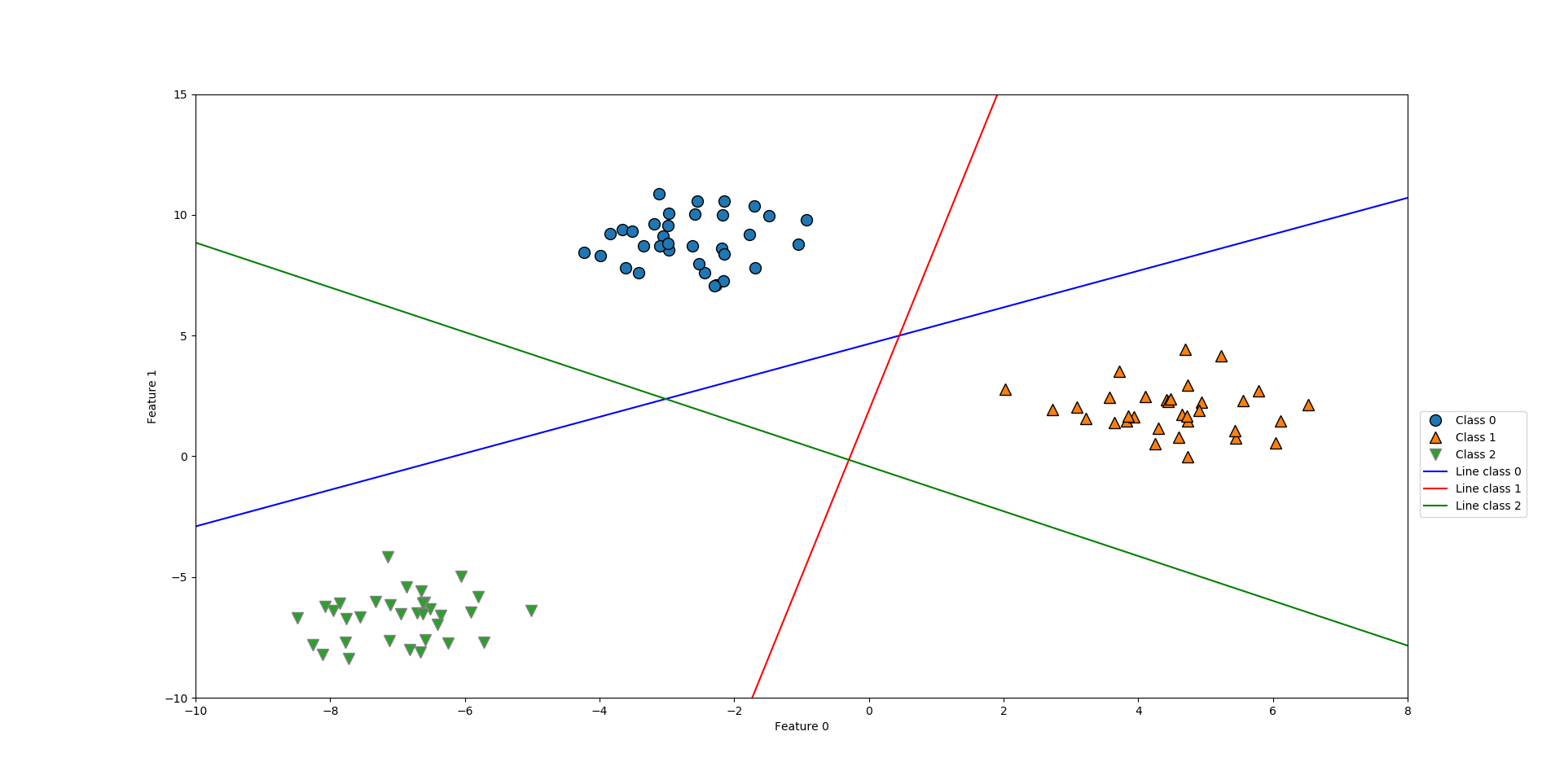
그래프 중간의 삼각형에 속한 데이터는 어떻게 될까요? 세 개의 모든 이진 분류기는 해당 데이터 포인트를 ‘나머지’라고 분류합니다. 만약 어떤 새로운 데이터 포인트가 이 영역에 속하게 되면 분류 공식에서 가장 큰 값을 갖게 되는, 즉 가장 가까운 line의 분류를 따라가게 됩니다.
다음의 소스 코드는 2차원 공간에 예측 결과를 표현한 것입니다.
| from sklearn.datasets import make_blobs X, y = make_blobs(random_state=42) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) from sklearn.svm import LinearSVC linear_svm = LinearSVC().fit(X, y) mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7) mglearn.discrete_scatter(X[:, 0], X[:, 1], y) line = np.linspace(-15, 15) for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']): plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color) plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1', 'Line class 2'], loc=(1.01, 0.3)) plt.xlabel("Feature 0") plt.ylabel("Feature 1") plt.show() |
결과)

장점, 단점, 매개변수
선형 모델은 학습과 예측이 빠르다는 장점이 있습니다. 즉, 데이터 셋이 매구 크거나 sparse data에 대해서도 잘 작동합니다. 수백, 수천, 수백만 개의 샘플로 구성된 데이터의 경우 LogisticRegression과 Ridge에서 solver=’sag’ 옵션을 사용할 수 있으며 이는 더욱 빠른 학습과 예측을 가능하게 합니다. 선형 모델의 또 다른 장점은 예측이 어떻게 이루어지는 지를 이해하기가 상대적으로 쉽다는 것입니다.
선형 모델은 특성의 수가 샘플의 수에 비해 클 때 잘 작동합니다. 때문에 매우 큰 데이터 셋에서 종종 사용됩니다만 낮은 차원의 데이터 셋에서는 다른 모델이 더 나은 일반화 성능을 보여줍니다.
선형 모델의 주요 매개변수는 정규화 변수인 alpha와 C입니다. alpha는 클수록, C는 작을수록 단순한 모델이 되며 특히 회귀 모델링에서 이런 매개변수를 조절하는 것이 매우 중요합니다. 대개 C와 alpha는 0.1, 1, 100과 같이 로그 스케일 상에서 선택됩니다. L1 정규화는 일부 특정 특성들만 중요하거나 결과적인 모델링이 해석이 쉽기를 바랄 때 이용되며, 이외에는 기본적으로 L2 정규화를 이용합니다.
'Python-머신 러닝 > Python-지도 학습 알고리즘' 카테고리의 다른 글
| 2. 지도 학습 알고리즘 (4) Decision Trees (0) | 2020.06.14 |
|---|---|
| 2. 지도 학습 알고리즘 (3) Naive Bayes Classifiers (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘 (1) k-Nearest Neighbors (k-NN) (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘-데이터 셋 다루기 (0) | 2020.06.13 |
| 1. 지도 학습 모델링의 기본 (0) | 2020.06.13 |