최종 수정 일자: 2020-06-14 15:04
해당 카테고리에 작성되는 글은 Introduction to Machine Learning with Python(파이썬 라이브러리를 활용한 머신 러닝)을 기반으로 작성되었습니다.

앞으로 지도 학습 알고리즘에 사용되는 여러 가지 모델링 및 최적화 기법에 대해서 알아보겠습니다. 각 모델링은 기초적인 최적화 기법을 담고 있으며 각각의 모델링에 대해 공통적으로 알아야 할 것은 다음과 같습니다.
- 각 알고리즘이 학습 데이터로부터 어떻게 학습하는지
- 학습 데이터에서 만들어진 모델을 기반으로 어떻게 예측을 하는지
- 각 알고리즘이 모델 복잡도를 어떻게 조절하는지
- 각 알고리즘의 장/단점 및 중요 매개변수와 설정에는 어떤 것들이 있는지
k-Nearest Neighbors
k-Nearest Neighbors, 줄여서 k-NN은 가장 단순한 머신 러닝 알고리즘입니다. 머신 러닝 모델을 구축하는 작업은 학습 데이터 셋을 저장하는 행위로만 이루어지며, 새로운 데이터 포인트에 대한 예측은 학습 데이터 셋에서 가장 가까운 데이터 포인트를 찾음으로써 이루어집니다. 즉, ‘가장 가까운 이웃’을 찾는 것이 모델의 예측 방식입니다.
k-NN 분류(classification)
가장 쉽고 단순하게 k-NN 알고리즘이 작동하는 방식은 시험 데이터 포인트와 가장 가까운 학습 데이터 포인트를 찾는 것입니다. 따라서 시험 데이터 포인트의 예측 결과인 결과값은 가장 가까운 학습 데이터 포인트의 결과값과 같게 됩니다. 분류의 경우 해당 학습 데이터 포인트의 클래스 라벨링을 따라갑니다. 아래의 소스 코드를 봅시다. 마찬가지로 numpy, matplotlib.pyplot, pandas, mgleran 모듈은 모두 임포트 된 상태입니다.
| mglearn.plots.plot_knn_classification(n_neighbors=1) plt.show() |
결과)
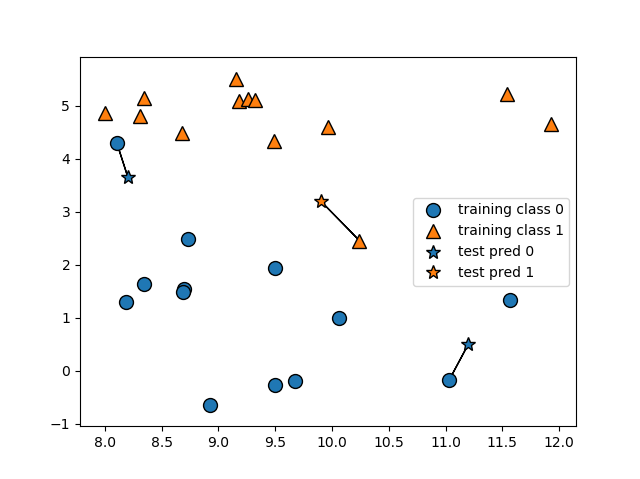
새로운 데이터 포인트인 별표 데이터가 가장 가까운 학습 데이터 포인트를 찾아서 해당 클래스로 라벨링되는 것을 확인할 수 있습니다. 여기서 좀 더 발전된 모델은 임의의 k개의 이웃을 고려하는 것입니다. 하나 이상의 이웃 데이터 포인트를 고려할 때, 라벨링은 ‘투표’를 통해 이뤄집니다. 즉, 가장 가까운 k개의 학습 데이터 포인터 중에서 더 많은 클래스를 따라서 시험 데이터가 라벨링 된다는 것입니다.
| mglearn.plots.plot_knn_classification(n_neighbors=3) plt.show() |
결과)
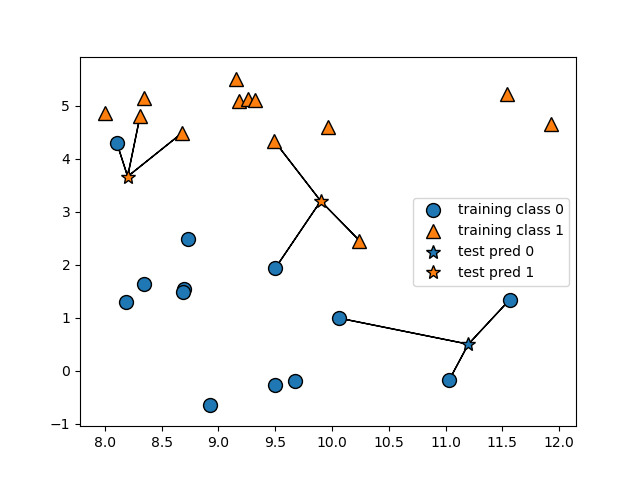
위의 설명은 모두 이진 분류에 대한 것이지만 k-NN 알고리즘은 다중 분류 문제에도 사용할 수 있습니다. 다중 분류에서는 각 클래스에 얼마나 많은 이웃들이 속해 있는지를 세어서 그 결과를 예측하게 됩니다.
이제 scikit-learn 패키지를 이용하여 k-NN 알고리즘을 적용해봅시다. 우선 우리가 보유한 데이터를 학습 데이터 셋과 시험 데이터 셋으로 나누어주어야 합니다. 이렇게 해야 모델의 일반화 성능(generalization performance)을 평가할 수 있기 때문입니다.
| from sklearn.model_selection import train_test_split X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) print(X_train) print(X_test) print(y_train) print(y_test) |
결과)
| [[ 8.92229526 -0.63993225] [ 8.7337095 2.49162431] [ 9.32298256 5.09840649] … [ 8.68937095 1.48709629]] [[11.54155807 5.21116083] [10.06393839 0.99078055] [ 9.49123469 4.33224792] [ 8.18378052 1.29564214] [ 8.30988863 4.80623966] [10.24028948 2.45544401] [ 8.34468785 1.63824349]] [0 0 1 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0] [1 0 1 0 1 1 0] |
위와 같이 학습 데이터 셋의 특성만을 담은 X_train, 그 결과값인 y_train과 시험 데이터 셋의 특성만을 담은 X_test, 그 결과값인 y_test가 할당됩니다. random_state=0으로 설정했기 때문에, 즉 임의로 데이터를 추출하는 것이 아니기 때문에 항상 같은 결과로 분할이 발생합니다. 다음으로 k-NN 알고리즘의 분류기(classifier) 클래스를 호출하여 학습을 시작하도록 하는 코드를 작성합니다.
| from sklearn.model_selection import train_test_split X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.neighbors import KNeighborsClassifier clf = KNeighborsClassifier(n_neighbors=3) |
이어서 시각화하는 코드를 추가합니다.
| from sklearn.model_selection import train_test_split X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.neighbors import KNeighborsClassifier clf = KNeighborsClassifier(n_neighbors=3) clf.fit(X_train, y_train) |
시험 데이터에 대한 예측을 하기 위해 해당 분류기 클래스에 속해 있는 predict 메서드를 호출합니다. 시험 데이터 셋의 각 데이터 포인트에 대해 k-NN 알고리즘을 거쳐 그 결과값(클래스 라벨링)을 제시합니다.
| from sklearn.model_selection import train_test_split X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.neighbors import KNeighborsClassifier clf = KNeighborsClassifier(n_neighbors=3) clf.fit(X_train, y_train) print("Test set predictions: {}".format(clf.predict(X_test))) |
결과)
| Test set predictions: [1 0 1 0 1 0 0] |
k-NN 알고리즘을 통한 모델링이 일반화를 잘 하는지를 평가하기 위해 해당 분류기 클래스 내의 score 메서드를 호출합니다.
| from sklearn.model_selection import train_test_split X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.neighbors import KNeighborsClassifier clf = KNeighborsClassifier(n_neighbors=3) clf.fit(X_train, y_train) print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test))) |
결과)
| Test set accuracy: 0.86 |
따라서 우리의 모델이 86%의 정확도를 갖는다는 것을 알 수 있습니다.
KNeighborsClassifier 분석
위에서 사용한 예시는 두 개의 특성을 갖는 2차원 데이터 셋이므로 xy평면 상에서 시각적으로 표현하여 모델링을 이해하고 분석할 수 있습니다. 각 클래스 라벨링 영역을 가르는 경계를 결정 경계(decision boundary)라 하며 이 경계를 기준으로 위의 데이터의 경우 class 0과 class 1이 구분됩니다.
| X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.model_selection import train_test_split X, y = mglearn.datasets.make_forge() X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) from sklearn.neighbors import KNeighborsClassifier fig, axes = plt.subplots(1, 3, figsize=(10, 3)) for n_neighbors, ax in zip([1, 3, 9], axes): # the fit method returns the object self, so we can instantiate and fit in one line clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y) mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4) mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax) ax.set_title("{} neighbor(s)".format(n_neighbors)) ax.set_xlabel("feature0") ax.set_ylabel("feature1") axes[0].legend(loc=3) plt.show() |
결과)
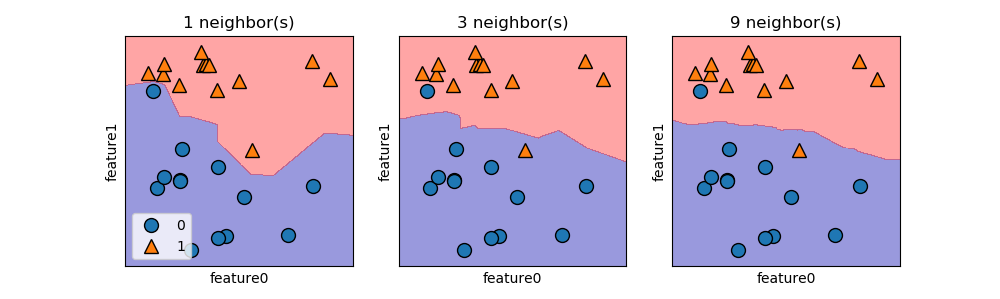
n_neighbors=1일 때 모델링이 학습 데이터 셋에 가까운 결정 경계를 만들어 냅니다. 즉, 학습 데이터 셋에 잘 맞는 복잡한 모델을 만든다는 것입니다. n_neighbors가 증가할수록 더 부드러운 결정 경계를 만들고 이는 학습 데이터 셋과는 조금 동떨어질 수 있는 단순한 모델을 만든다는 것입니다. 가령 n_neighbors=학습 데이터 포인트의 수가 되면 학습 데이터 셋 내에서 수가 많은 결과 라벨링만 반환하게 됩니다.
위의 모델 복잡도와 일반화 사이의 관계를 확인하는 코드를 짜봅시다. 이때 실제 데이터 셋인 Breast Cancer 데이터 셋을 이용해봅시다. 학습 데이터 셋과 시험 데이터 셋으로 데이터 셋을 분할하고 모델의 성능을 각기 다른 n_neighbors에 대해서 평가해봅시다.
| from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=66) training_accuracy = [] test_accuracy = [] # try n_neighbors from 1 to 10 neighbors_settings = range(1, 11) from sklearn.neighbors import KNeighborsClassifier for n_neighbors in neighbors_settings: # build the model clf = KNeighborsClassifier(n_neighbors=n_neighbors) clf.fit(X_train, y_train) # record training set accuracy training_accuracy.append(clf.score(X_train, y_train)) # record test set accuracy test_accuracy.append(clf.score(X_test, y_test)) plt.plot(neighbors_settings, training_accuracy, label="training accuracy") plt.plot(neighbors_settings, test_accuracy, label="test accuracy") plt.ylabel("Accuracy") plt.xlabel("n_neighbors") plt.legend() plt.show() |
결과)
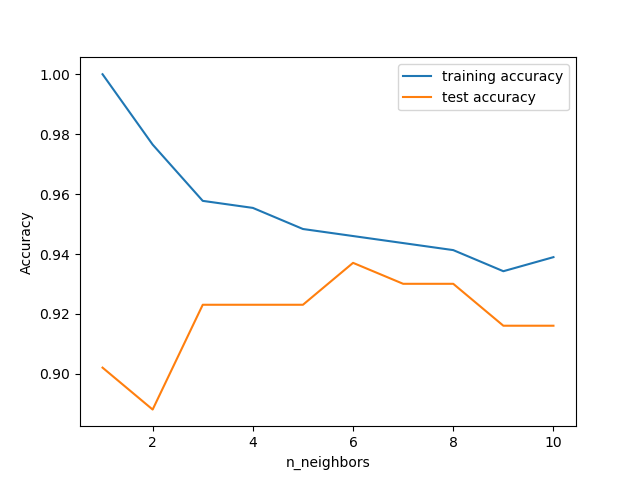
더 큰 n_neighbors가 고려될수록 모델이 더욱 단순해지며 학습 데이터 셋에 대한 학습 정확도가 떨어지게 됩니다. n_neighbors=1인 경우 시험 정확도가 더 큰 n_neighbors를 사용할 때보다 떨어지는데 이는 해당 모델이 지나치게 학습 데이터 셋에 맞춰져 있는, 아주 복잡한 모델이기 때문에 일어납니다. 반대로 n_neighbors=10의 경우 모델이 지나치게 단순해져 성능이 더 떨어지는 것을 확인할 수 있습니다.
k-NN 회귀(regression)
언뜻 k-NN은 분류 문제에만 사용할 수 있는 알고리즘처럼 생각될 수도 있습니다. 하지만 k-NN은 회귀 문제에도 사용할 수 있으며 이때 가장 가까운 이웃 데이터 포인트의 값을 추종하는 식으로 학습을 진행합니다. n_neighbors=1의 경우에 대한 예측은 다음의 소스 코드를 참고하면 됩니다.
| mglearn.plots.plot_knn_regression(n_neighbors=1) plt.show() |
결과)
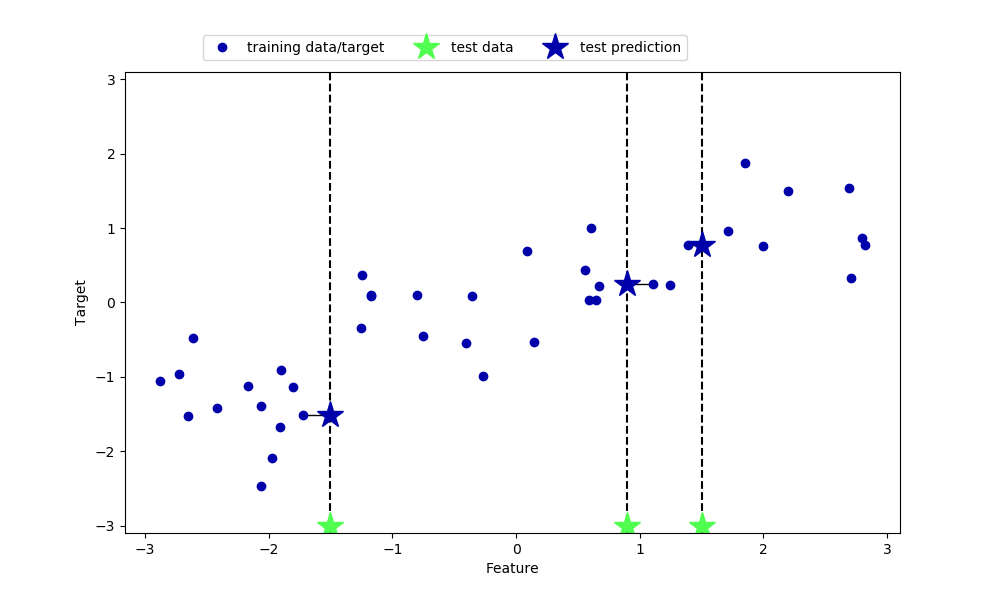
즉, 시험 데이터 포인트와 가장 가까운 학습 데이터 포인트의 결과값으로 예측값을 반환한다는 것을 알 수 있습니다. n_neighbors를 1보다 크게 가져가면 가장 가까운 n_neighbors개의 이웃들의 결과값의 평균으로 예측값을 반환합니다.
| mglearn.plots.plot_knn_regression(n_neighbors=3) plt.show() |
결과)
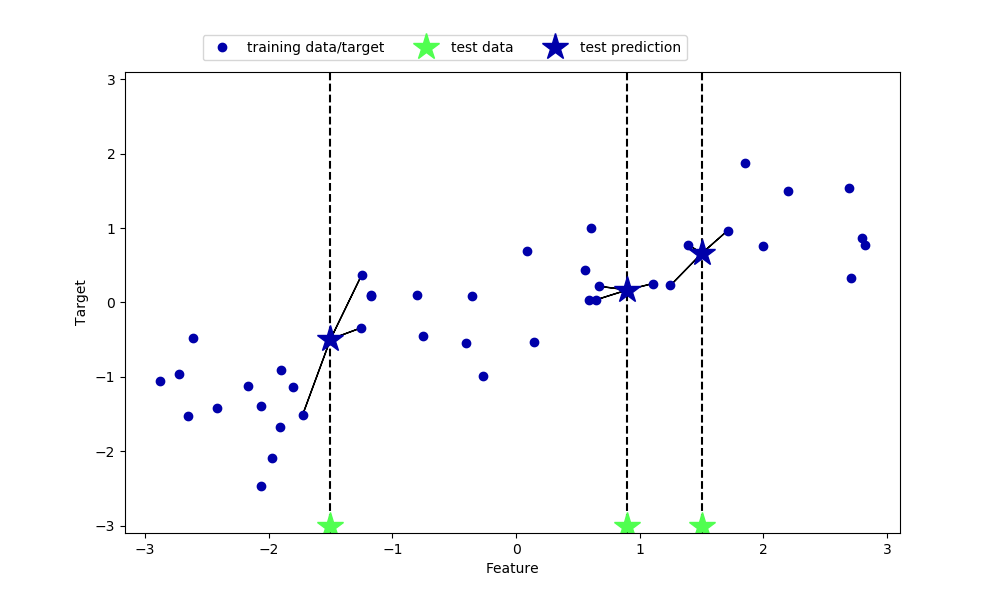
scikit-learn의 k-NN 회귀 알고리즘은 KNeighborsRegressor 클래스로 시행할 수 있습니다.
| from sklearn.neighbors import KNeighborsRegressor X, y = mglearn.datasets.make_wave(n_samples=40) # split the wave dataset into a training and a test set from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # instantiate the model and set the number of neighbors to consider to 3 reg = KNeighborsRegressor(n_neighbors=3) # fit the model using the training data and training targets reg.fit(X_train, y_train) print("Test set predictions:\n{}".format(reg.predict(X_test))) print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test))) |
결과)
| Test set predictions: [-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382 0.35686046 0.91241374 -0.44680446 -1.13881398] Test set R^2: 0.83 |
회귀 문제에서 KNeighborsRegressor 클래스의 score 메서드는 결정 계수(coefficient of determination)인 R2 값을 반환합니다. 1에 가까울수록 완벽한 예측입니다.
KNeighborsRegressor 분석
1차원 데이터 셋에 대해 예측이 어떤식으로 이루어지는지 시각화할 수 있습니다.
| X, y = mglearn.datasets.make_wave(n_samples=40) from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) fig, axes = plt.subplots(1, 3, figsize=(15, 4)) # create 1000 data points, evenly spaced between -3 and 3 line = np.linspace(-3, 3, 1000).reshape(-1, 1) from sklearn.neighbors import KNeighborsRegressor for n_neighbors, ax in zip([1, 3, 9], axes): # make predictions using 1, 3, or 9 neighbors reg = KNeighborsRegressor(n_neighbors=n_neighbors) reg.fit(X_train, y_train) ax.plot(line, reg.predict(line)) ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8) ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8) ax.set_title("{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(n_neighbors, reg.score(X_train, y_train), reg.score(X_test, y_test))) ax.set_xlabel("Feature") ax.set_ylabel("Target") axes[0].legend(["Model predictions", "Training data/target", "Test data/target"], loc="best") plt.show() |
결과)
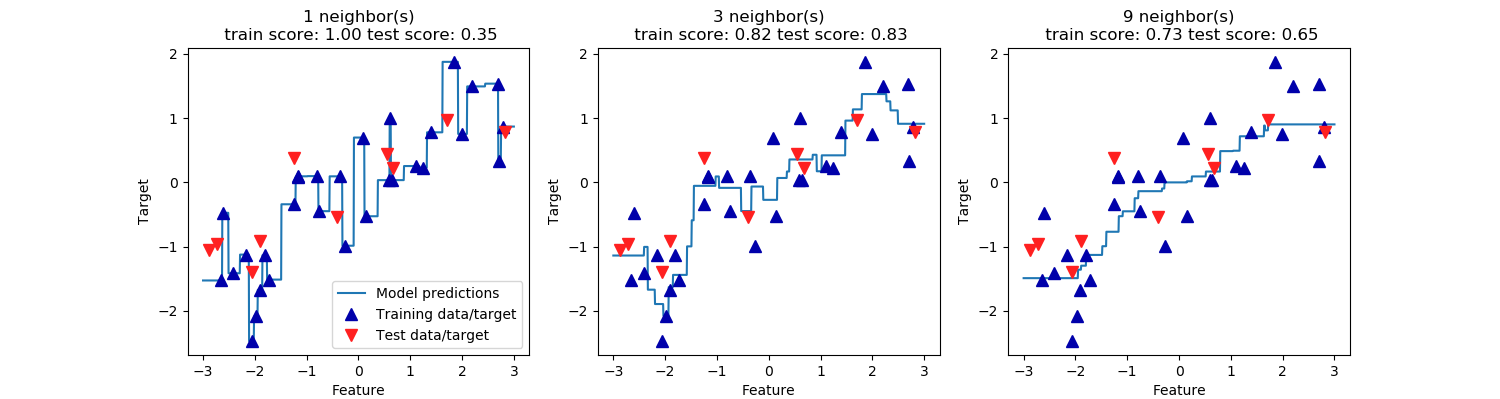
단일 neighbor를 사용할 때 학습 데이터 셋 내의 각 포인트가 시험 데이터 포인트의 예측에 직접적으로 영향을 미칩니다. 더 큰 n_neighbors는 부드러운 예측을 가능하게 하지만 학습 데이터에도 잘 맞지 않게 될 수 있습니다.
장점, 단점, 매개변수
k-NN 알고리즘의 장점은 무엇보다도 알고리즘의 이해가 쉬우면서도 별다른 조정 없이도 합리적인 성능을 보여준다는 것에 있습니다. k-NN은 더 복잡한 머신 러닝 테크닉을 사용하기 이전에 기본적으로 사용해볼만한 알고리즘으로 모델 구축이 매우 빠르다는 측면도 장점으로 작용합니다.
단점은 특성의 수 또는 데이터 포인트가 많아질수록, 즉 학습 데이터 셋이 커질수록 예측이 느리다는 것입니다. 또한 대 부분의 특성이 0인 spase dataset과 같은 특정 데이터 셋에서는 특히나 잘 작동하지 않습니다.
원론적으로 KNeighborsClassifier 및 KNeighborsRegressor의 중요한 두 가지 매개변수는 첫째, 사용할 이웃의 수와 둘째, 데이터 포인트 사이의 거리를 어떻게 측정할 것인가입니다. 관용적으로 n_neighbors는 3 또는 5의 값이 잘 작동하지만 이 매개변수를 조절할 수 없는 것은 아닙니다. 적절한 거리 측정 방법을 선택하는 것은 지금 당장의 학습의 범위를 넘어서는 것이므로 고려하지 않겠습니다만, 기본적으로는 Euclidean distance를 이용합니다.
'Python-머신 러닝 > Python-지도 학습 알고리즘' 카테고리의 다른 글
| 2. 지도 학습 알고리즘 (4) Decision Trees (0) | 2020.06.14 |
|---|---|
| 2. 지도 학습 알고리즘 (3) Naive Bayes Classifiers (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘 (2) Linear Model (0) | 2020.06.14 |
| 2. 지도 학습 알고리즘-데이터 셋 다루기 (0) | 2020.06.13 |
| 1. 지도 학습 모델링의 기본 (0) | 2020.06.13 |